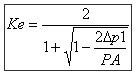For the compressible fluids (air, gas, steam, etc), the parameters "volume, density, viscosity", vary in a very significant way according to the pressure and of the temperature of use.

The density of a gas, which follows the Mariotte's Law, is given by the following formula:

• p = density of gas in kg/m 3
• mM = molar mass of gas (kg/kmol)
• P = Absolute pressure (Pa)
• T = Absolute temperature (K)

For standard gases located at 0°C and 101325 Pa.

.

Density

This density W is expressed in kg/m3 and has as an expression:

• Mref = density of gas expressed in kg/m3 (with 0°C under 101325 Pa)
• P = relative pressure of use of the fluid in Pa.
• t = represents the temperature of the air in °C.
• P = relative pressure of use of the fluid in Pa.
• Pb = barometric pressure in Pa.

Volumic flow (Correction compared to the basic flow)

By stating a unit of flow such as normal m3 of a gas fluid, there are two parameters which are critical for the definition of the unit flow. They are the pressure and the temperature.

All in all, the pressure is always 1013.25 mbar (KPa), 760 mm hectograms (hg) or 14.7 psia, which all are equivalent. However, the standard temperature changes from one country to another modifying to a significant degree the real flow.

In Europe
The volume of reference or the Normal cubic meter is often characterized by the abbreviation m³(n) or (Nm3).

This indication means that the cubic meter is given under the conditions of temperature to 0°C, under an absolute pressure of 101300 Pascals, i.e. under the normal atmospheric pressure on the sea level.

In USA
LThe gas flows are measured with 70° F (21.1° C, 294.25 K) with 14.7 psia. (1013.25 mbar). Under these conditions, the pressure is constant but the differential of temperature generates a difference in flow roughly of 7.7% if no conversion of volume is made without taking into account this change of temperature.

This is even more confused in the manufacturers of the equipment by using various names for the same unit or the same name for the various units.

Under the conditions of temperature and pressure of use, the correction of volume-flow compared to the flow of reference is carried out by the following formula:

• Qc = Volume-flow corrected in m3/h (measured under the new basic conditions)
  
• Q = Volume-flow of reference in m3/h (Either under an atmospheric pressure of 101325 Pa)
  
• T = Represents the surrounding temperature of the air in °C.
  
• P = relative pressure of use of the Pa.
  
• Pb = average barometric Pa pressure at altitude.

V1 = (V2 x T1) / T2

With:

• V = Gas flow
• T = Temperature (Kelvin)

Contrary to calculations of the pressure losses for the liquid fluids (regarded practically as incompressible) the pressure loss due to the flow of a gas fluid (air, gas, steam, etc.) be accompanied by an expansion which results in an increase in the flow (i.e. speed), a reduction in the density and an increase in dynamic viscosity:

With in this expression:

• Ke = Correction of expansion
• Dp1 = Only linear pressure loss calculated as if the fluid were incompressible (singular pressure losses not included)
• PA = Absolute Pressure at point A, i.e. the entry of piping, or the origin of the section considered (absolute pressure)

The atmospheric pressure known as "normal", i.e. on the sea level is 101 325 Pa

The more we go up in altitude and the more the atmospheric pressure decreases. This pressure according to altitude has as a value:

• A = Altitude in m.
• Pb = Atmospheric pressure at altitude in Pa.
• 101325 = Atmospheric pressure at the sea level.

The gain (or this loss) of relative pressure will be taken into account for the evaluation of the pressure losses on the open circuits, such as for example a gas feeding.

With:

• G = Gain or loss of pressure in mmCE
• H = Difference of height in m
• wair = Density of the ambient air, expressed in kg/m3 (according to the level of altitude)
• wg = Density of gas, expressed in kg/m3 (according to the temperature and the pressure of use)

Last update: